• 数据结构：计算机存储、组织数据的方式
• 数据库 CRUD 操作：
  增加（Create）、读取查询（Retrieve）、更新（Update）、删除（Delete）

数组（Array）

• 擅长做查询和修改，不擅长做增加（可能需要扩容）和删除（移位）
• 在随机访问时性能最好

// 基于数组的线性表（集合）
public class MyArrayList {
    private Object[] elementData;
    private int size;
    private static final int DEFAULT_CAPACITY = 10;

    public MyArrayList() {
        this(DEFAULT_CAPACITY);
    }
    
    public MyArrayList(int initiallyCapacity) {
        if (initiallyCapacity < 0) {
            throw new IllegalArgumentException("Illegal Capacity: " + initialCapacity);
        }
        elementData = new Object[initiallyCapacity];
    }
}

// 1. 在形参包含索引的方法内，检查传入的索引是否越界
// 2. 写每个方法时，最后要判断该方法是否会改变 size 的值

#链表（Linked List）

• 擅长做增加和删除（头和尾），不擅长做查询和修改
• 在执行插入、删除操作时有较好的性能
• 单向链表、双向链表

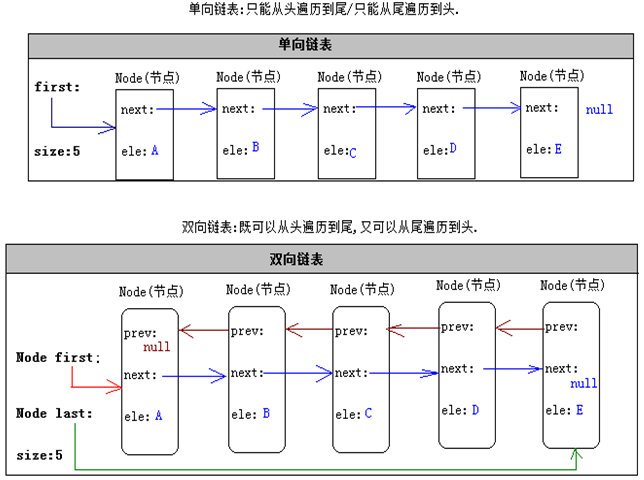
// 基于双向链表的线性表（集合）
public class MyLinkedList {
    private Node first; // 链表的第一个节点
    private Node last; // 链表的最后一个节点
    private int size; // 节点的数量
    
    // 删除链表中第一次出现的元素 o
    public boolean removeFirstOccurrence(Object o) {
        Node currentNode = first;
        while (currentNode != null) {
            if (currentNode.ele.equals(o)) {
                // 删除节点
                if (currentNode == first) {
                    currentNode.next.prev = null;
                    first = currentNode.next;
                    size--;
                    return true;
                } else if (currentNode == last) {
                    currentNode.prev.next = null;
                    last = currentNode.prev;
                    size--;
                    return true;
                } else {
                    currentNode.prev.next = currentNode.next;
                    currentNode.next.prev = currentNode.prev;
                    size--;
                    return true;
                }
            }
            currentNode = currentNode.next;
        }
        return false;
    }
    
    // 返回链表的字符串表示形式
    public String toString() {
        if (size == 0) {
            return "[]";
        }
        Node currentNode = first;
        StringBuilder sb = new StringBuilder();
        sb.append("[");
        for (int i = 0; i < size; i++) {
            sb.append(currentNode.ele);
            if (i != size - 1) {
                sb.append(", ");
            } else {
                sb.append("]");
            }
            currentNode = currentNode.next;
        }
        return sb.toString();
    }
    
    // 内部类 Node
    private static class Node {
        Node prev; // 上一个节点
        Node next; // 下一个节点
        Object ele; // 节点中的数据
        
        Node(Object ele) {
            this.ele = ele;
        }
    }
}

// 1. 先修改当前节点，再修改当前节点的上一节点、当前节点的下一节点，最后修改链表的 first、last
// 2. 写每个方法时，最后要判断该方法是否会改变 size 的值

栈（Stack）

• 一种运算受限的线性表，仅允许在表的一端进行插入和删除运算
• 后进先出（LIFO）
• 进栈、入栈或压栈；出栈或退栈
• 底层可以数组来存储，也可以使用链表来存储

队列（Queue）

• 一种特殊的线性表，只允许在表的后端（rear）进行插入操作，在表的前端（front）进行删除操作
• 单向队列（Queue）：先进先出（FIFO），只能从队列尾插入数据，只能从队列头删除数据
• 双向队列（Deque）：可以从队列尾/头插入数据，也可以从队列头/尾删除数据

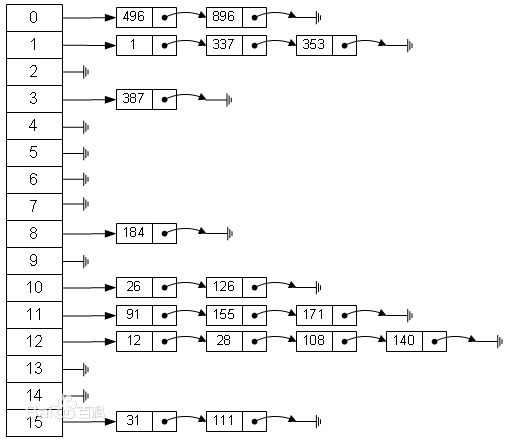
哈希表（Hash Table）

• 元素的值和索引存在对应的关系的数组
• 元素值 --> Hash 函数 --> 哈希码 --> 某种映射关系（压缩映射） --> 元素存储索引
• 可以直接根据该元素的 hashCode 值计算出该元素的存储位置，因此具有很好的存取和查找性能

堆（Heap）

图（Graph）

树（Tree）

• 适用于范围查找，一般用来做索引